Banc d'optique virtuel
Logiciel Cocoa de simulation de système optique à lentilles. Une occasion ludique de mesurer la grande difficulté que représente la conception d'un objectif photographique ! J'ai porté ce projet en html/Javascript, il est disponible ici !
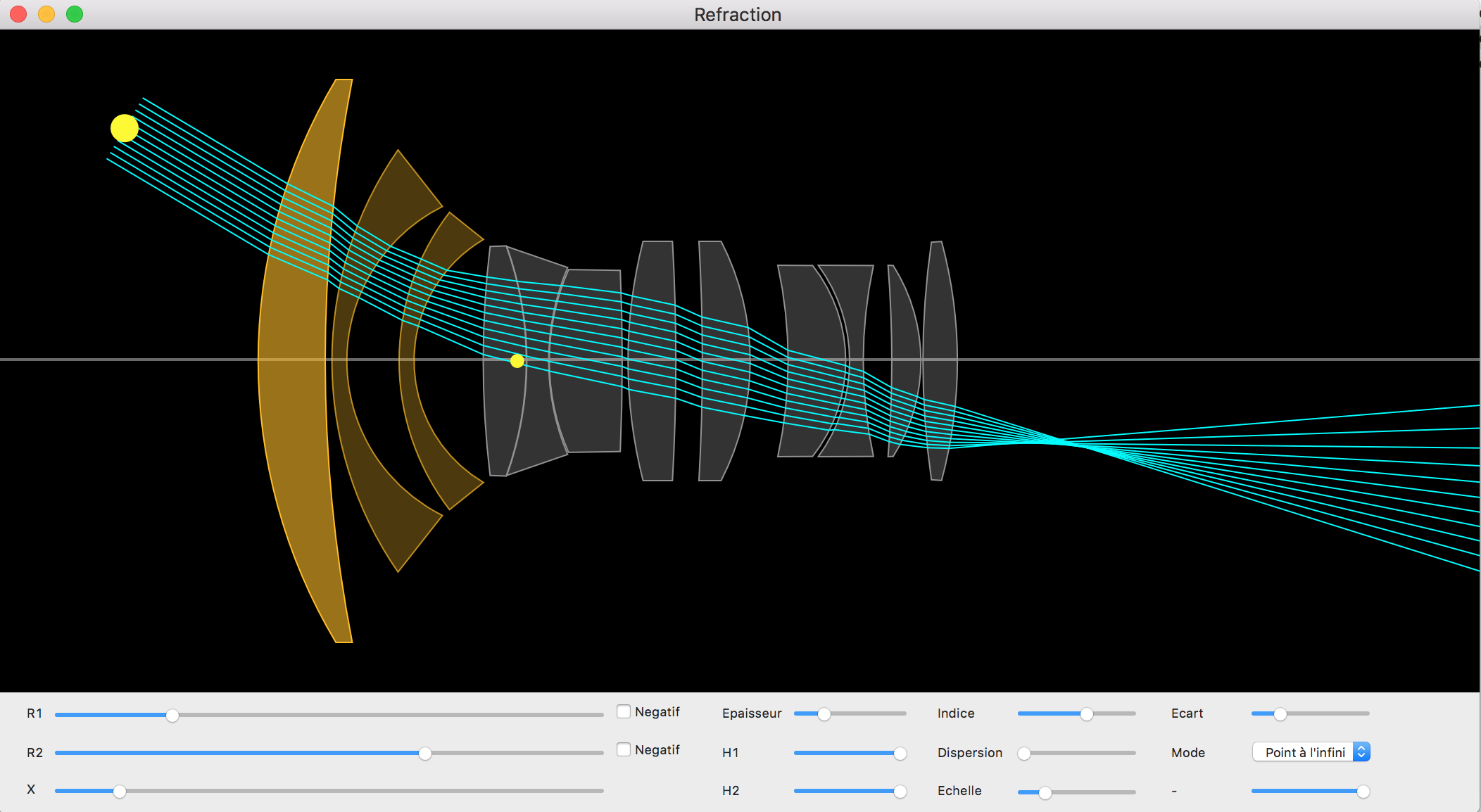
Cela faisait longtemps que je souhaitais faire un tel soft, c'est à dire résoudre deux difficultés :
- Traiter avec les lentilles réelles et non les "lentilles minces" théoriques. C'est à dire abandonner les lois de conjugaison simples.
- Calculer le chemin d'un rayon à travers une série de lentilles arbitraire et possible à éditer dynamiquement .
Cela est réalisé en considérant les rayons comme une succession de trajets entre deux dioptres (sphériques). Chaque trajet est caractérisé par une équation de droite. On calcule ensuite l'intersection avec le prochain dioptre (les 1er et dernier trajets sont calculés différemment) :
Équation du rayon incident : $$ y=ax+b $$ Équation du prochain dioptre : $$ \left( x-o_x \right)^{2}\; +\; \left( y-o_y \right)^{2}\; =\; R^{2} $$ Paramètres de l'équation du second degré : $$ Ax^2 + Bx + C = 0 $$ $$ A\; =\; a^{2}\; +\; 1 $$ $$ B\; =\; 2ab\; -\; 2o_x\; -\; 2ao_y $$ $$ \mbox{C}\; =\; b^{2}-2bo_y+o_y^{2}+o_x^{2}-R^{2} $$ Solutions de l'équation (on en élimine une car on connait l'ordre des dioptres) :
$$ \Delta \; =\; B^{2}-4A\mbox{C} $$ $$ solutions \; =\frac{\; -B\; ±\; \sqrt{\Delta} }{2A} $$
À chaque rencontre du rayon avec un dioptre, on calcule l'angle d'incidence du rayon par rapport à la normale à la tangente au dioptre en ce point. La relation de Snell-Descartes permet de connaître l'angle de sortie du rayon réfracté :
$$ indice_{avant} sin(angle_{incident}) = indice_{après} sin(angle_{réfracté}) $$
À partir de cet angle (considéré dans le repère du système) et du point de départ, on calcule les nouveaux paramètres a et b de l'équation de droite de faisceau tel que :
$$ a = tan(angle_{sortie}) $$ $$ b = y - ax $$
La boucle peut recommencer avec le prochain dioptre. Si aucune intersection n'existe avec le prochain dioptre, des valeurs indéterminées apparaissent (NaN) ce qui empêche toute poursuite du calcul. Le rayon alors ne s'affichera pas.
Le logiciel possède des touches de contrôle :
- + = créer une lentille
- D = dupliquer la lentille sélectionnée
- O = importer une lentille
- S = sauver la lentille dans l'application
- E = exporter une lentille (ajouter extension .lense)